23. Taylor Series

e. Taylor Remainder

If \(a\) is in an open interval \(I\) and \(M \ge |f^{(k+1)}(c)|\) for all \(c\) in the interval \(I\), then the Taylor remainder of degree \(k\) centered at \(x=a\) satisfies \[ |R_k f(x)| \le \dfrac{M}{(k+1)!}|x-a|^{k+1} \] for all \(x\) in the interval \(I\). The quantity on the right is called the Taylor bound on the remainder.

2. Approximation Error

If \(f(x)=\sinh x=\dfrac{e^x-e^{-x}}{2}\) is approximated by its \(9^\text{th}\) degree Maclaurin polynomial \[ \sinh x\approx T_9\sinh x =x+\dfrac{1}{3!}x^3+\dfrac{1}{5!}x^5+\dfrac{1}{7!}x^7+\dfrac{1}{9!}x^9, \] find an upper bound on the maximum error in the approximation on the interval \((-2,2)\).

The graphs (at two scales) of \(\sinh x\) (in BLUE) and \(T_9\sinh x=x+\dfrac{1}{3!}x^3+\dfrac{1}{5!}x^5+\dfrac{1}{7!}x^7+ \dfrac{1}{9!}x^9\) (in RED) are

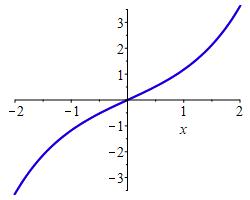
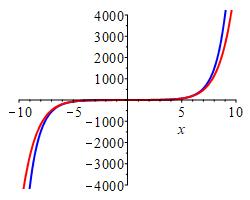
On the interval \((-2,2)\) it is impossible to see any difference. The terms of the series all have the same sign (positive if \(x\) is positive and negative if \(x\) is negative). So we cannot use an alternating series bound.

xxx To use the Taylor bound on the remainder \(R_9f(x)\), we take \(k=9\) and \(a=0\). Then \[ |R_9f(x)| \le \dfrac{M}{(k+1)!}|x-a|^{k+1} = \dfrac{M}{10!}|x|^{10} \] where \(M \ge |f^{(10)}(c)|\) for \(c\in(-2,2)\). To find \(M\), notice that the derivatives of \(\sinh x\) alternate between \(\cosh x=\dfrac{e^x+e^{-x}}{2}\) and \(\sinh x\). So \(f^{(10)}(c)=\sinh c\). On the interval \((-2,2)\), the largest value of \(|\sinh c|\) occurs at \(c=2\) (and \(c=-2\)). So we take \(M\) as \[ M=|f^{(10)}(2)|=|\sinh2|\approx 3.62 \] Also, on the interval \((-2,2)\), the largest value of \(|x|\) is \(2\). So \[ |R_9f(x)| \le \dfrac{M}{10!}|x|^{10} \le \dfrac{\sinh 2}{10!}2^{10} \approx.001 \]